Graph Theory Haiku

My most recent talk in UVic’s discrete math seminar presented three poetic proofs by Adrian Bondy… and three actual poems summarizing the ideas in each one.

Ore’s Theorem

A red-blue $K_n$:
bluest Hamilton circuit
lies fully in $G$.

Ore’s theorem states:

Let $G$ be a simple graph on $n \geq 3$ vertices such that $d(u) + d(v) \geq n$ for any nonadjacent $u, v$. Then $G$ contains a Hamilton cycle.

Bondy’s proof is roughly as follows. Colour the edges of $G$ blue and add red edges to make a complete graph. The complete graph on $n \geq 3$ vertices has no shortage of Hamilton cycles, so choose one and label it $v_1 v_2 \ldots v_n v_1$.

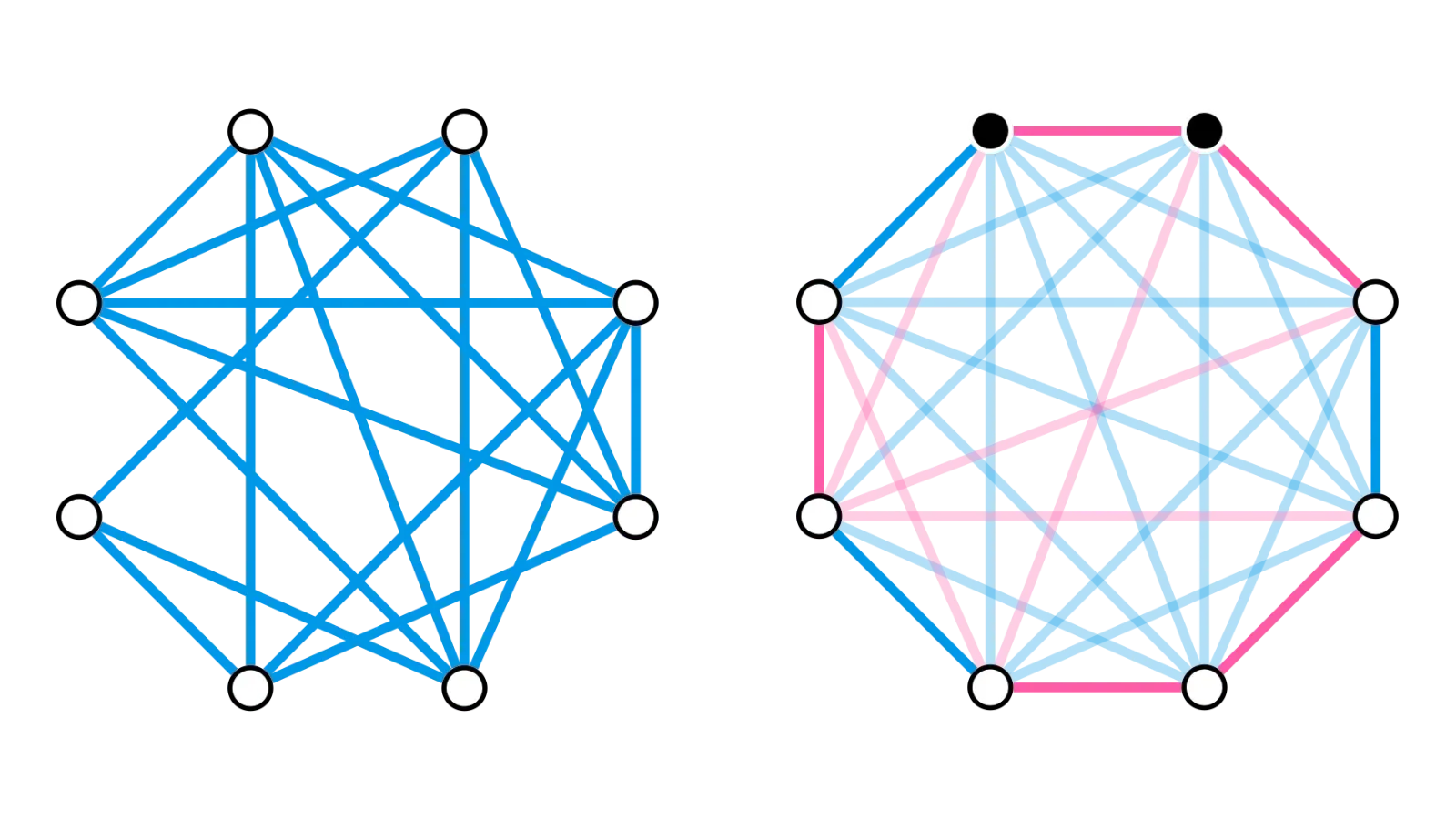
Consider the blue neighbours of $v_1$ on the cycle, and then move one vertex to the right along the cycle so you’re looking at the set

There are $d_G(v_1)$ of these vertices, and if $v_1 v_2$ is red (i.e. $v_1$ and $v_2$ are nonadjacent in $G$), then the theorem’s hypothesis tells us that

Since $v_2$ has only $n-1-d_G(v_2)$ red neighbours and is not itself in $S$, that means at least one vertex $v_{i+1} \in S$ is a blue neighbour of $v_2$. We can now replace $v_1 v_2$ and $v_i v_{i+1}$ in the cycle with the two blue edges $v_1 v_2$ and $v_2 v_{i+1}$ to get a Hamilton cycle of $K_n$ with at least one more blue edge than we had before.

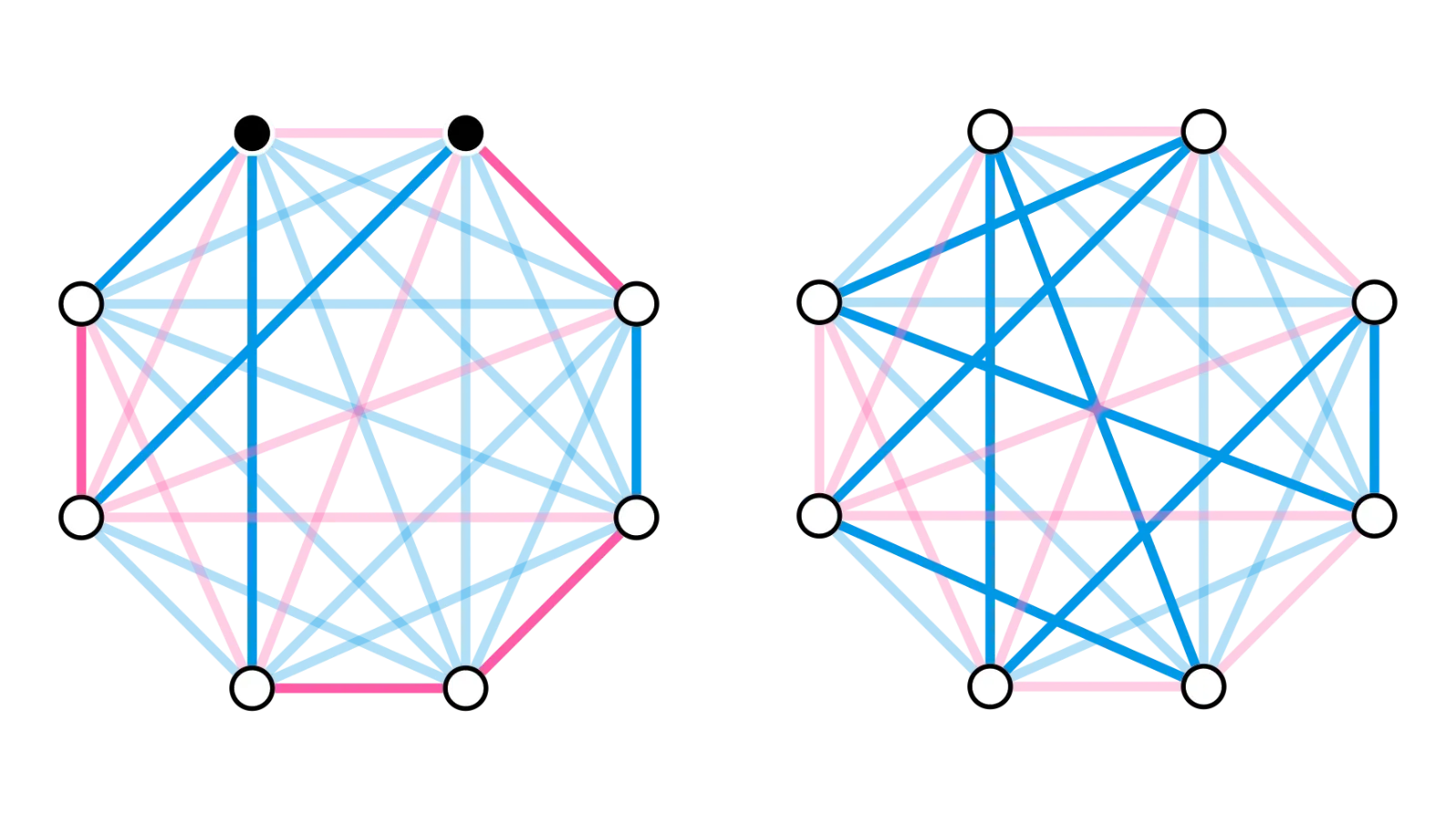
We can make the same argument again and again until we have a Hamilton cycle of $K_n$ with no red edges. The cycle being blue means it lies entirely in $G$, which proves the theorem.

Brooks’ Theorem

Greedily colour,
ensuring neighbours follow
all except the last.

Choose the last vertex wisely:
friend of few or of leaders.

Brooks’ Theorem says:

If $G$ is connected and is not an odd cycle or a clique, then $\chi(G) \leq \Delta(G)$.

If $G$ is not regular, Bondy colours it as follows. Let $r$ be a vertex of smaller-than-maximum degree. If we consider the vertices in the reverse order of a depth-first search rooted at $r$, each vertex other than $r$ has at least one neighbour later in the order and at most $d(v)-1$ neighbours earlier. Greedily colouring in this order will assign one of the first $d(v) \leq \Delta(v)$ colours to each $v \neq r$, and at least one colour remains available for $r$ since its degree is strictly smaller than $\Delta(G)$.

If $G$ is regular, there are a few cases. If it has a cut vertex, we can break the graph into two (non-regular) parts, colour each of them separately, and put them back together. If it has a depth-first tree that branches at some point, then Bondy constructs an ordering similar to the one for the non-regular case: if $x$ has distinct children $y, z$ in the tree, $G$ can be ordered so $y$ and $z$ come first, $x$ comes last, and every other vertex has at least one neighbour later on in the order. A greedy colouring according to this order uses at most $\Delta(G)$ colours.

Finally, if $G$ is regular, 2-connected, and all of its depth-first trees are paths, it turns out that $G$ must be a chordless cycle, a clique, or a complete bipartite graph. Since bipartite graphs have $\chi(G) = 2 \leq \Delta(G)$, the only exceptions to the theorem are odd cycles and cliques.

Vizing’s Theorem

Induction on $n$.
Swap available colours
and find SDR.

Vizing’s theorem says:

For any simple graph $G$, the edge chromatic number $\chi'(G)$ is at most $\Delta(G)+1$.

The proof is by induction on the number of vertices; pick a vertex $v$ and start with a $(\Delta(G)+1)$-edge-colouring of $G-v$.

Ideally, we could just colour the edges around $v$ and extend the edge-colouring to one of $G$. Those colours would need to be a system of distinct representatives (SDR) for the sets of colours still available at each of the neighbours of $v$.

If we can’t find a full SDR, then we can still try to colour as many of $v$‘s edges as possible. Then, if an edge $uv$ is still uncoloured, we can follow a proof of Hall’s Theorem to get a set of coloured edges $u_1 v, u_2 v, \ldots, u_k v$ such that:

• $uv$ can’t be coloured because there are fewer than $k+1$ total colours among those available at $u$ and $u_1, u_2, \ldots, u_k$ in the colouring of $G-v$, but
• if you un-colour any one of the edges and swap around the colours of the other ones, it would become possible to colour $uv$.

Note also that

• regardless of how we assign $\Delta(G)+1$ colours to edges of $G$, each vertex will have at least one colour left unused by the edges around it.

The first and third facts put together tell us that some colour (say, blue) is available at two vertices among $u$ and $u_1, u_2, \ldots, u_k$.

The second fact implies that any colour (e.g. red) still available at $v$ can’t be available at any of the $u_i$, as otherwise we could swap around the colours to colour $uv$ and then use red for $u_i v$.

Look at the subgraph $H$ of $G$ formed by the red and blue edges — it’s made of paths and even cycles. We know that $v$ is incident with a blue edge but not a red one, so it’s the end of a path in $H$.

We also know that there are two vertices among $u, u_1, u_2, \ldots, u_k$ that are incident with a red edge but not a blue one; those are also ends of paths in $H$. The paths might be the same as each other, and one might be the same as $v$‘s path, but the important thing is that we have a red-blue path where at least one of the ends is a neighbour $u'$ of $v$ and the other end is any vertex other than $v$.

We can now modify the colouring of $G-v$ to swap red and blue along this path, which frees up red at $u'$. If $u'$ is $u$ itself, then we can colour $uv$ red; otherwise, we can uncolour $u'v$, swap colours around to colour $uv$, and use red for $u'v$.

Either way, we’ve shown that the modified colouring of $G-v$ has a larger set of distinct representatives than the original colouring. By repeating this process, we eventually find a colouring of $G-v$ that has a full SDR — and therefore can be extended to a full $(\Delta(G)+1)$-edge-colouring of $G$.