
A visual proof that 216 is a sum of three cubes.

A visual proof that 216 is a sum of three cubes.

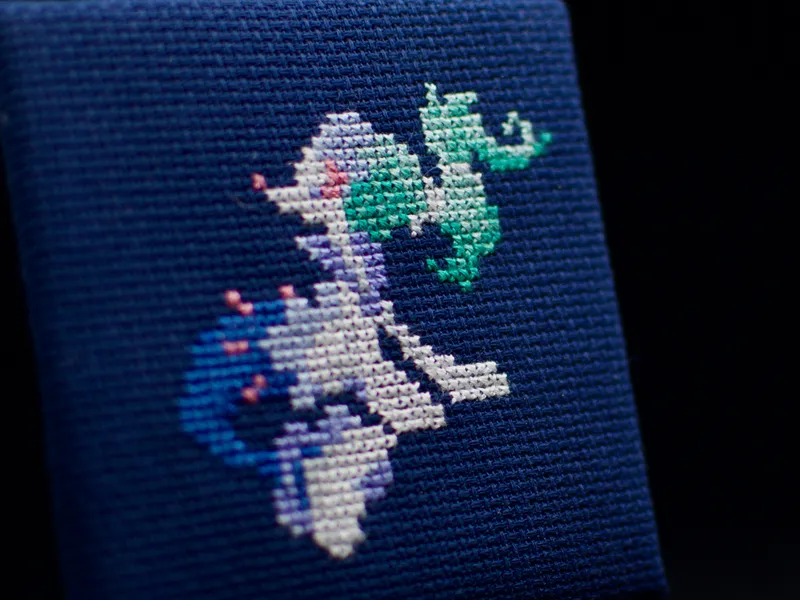



I’ve dipped my toes into the fediverse! You can follow me from Mastodon, Firefish, or other ActivityPub-compatible social media platforms at @rchurchley@chrosy.net.

The Legend of Zelda: Tears of the Kingdom calls your attention to the sky… but there’s more weird stuff up there than just the floating islands.

I recently went for a walk in təmtəmíxʷtən (Belcarra), and when I got to… wait, what’s that weird derelict building in the distance?

Julius Caesar’s given name was Gaius. “Julius” and “Caesar” were both family names (Caesar being a branch of the Julia family).

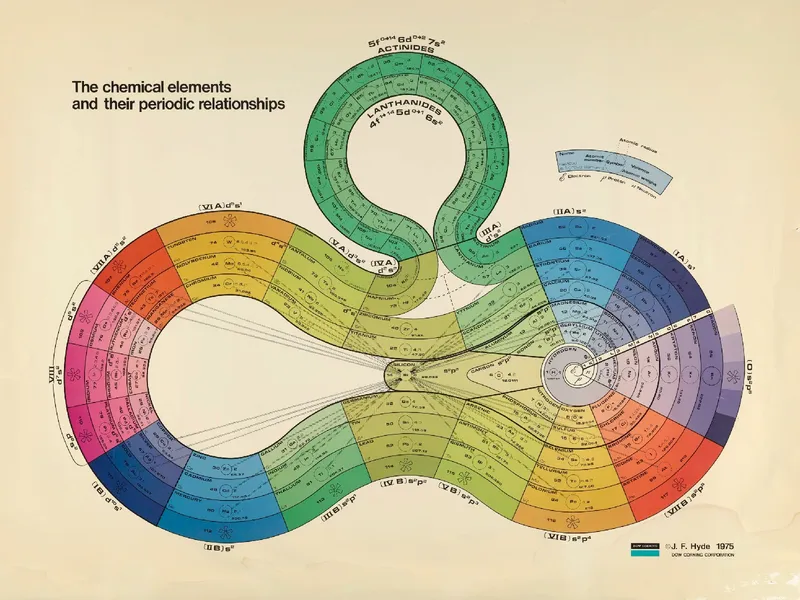
The standard Periodic Table is an iconic data visualization, but it’s not the only way to represent the relationships between elements. This beautiful “ribbon” version was designed by James Hyde in the 1970s.

Between cabbage, lettuce, maple, and holly, two plants are in the rosid clade (related to roses) and two are in the asterid clade (related to sunflowers). Can you guess which is which?

Every new emoji starts with a formal proposal justifying why it should exist.
The proposal for 🫵 starts with four pages of the history of people pointing at the viewer in art.
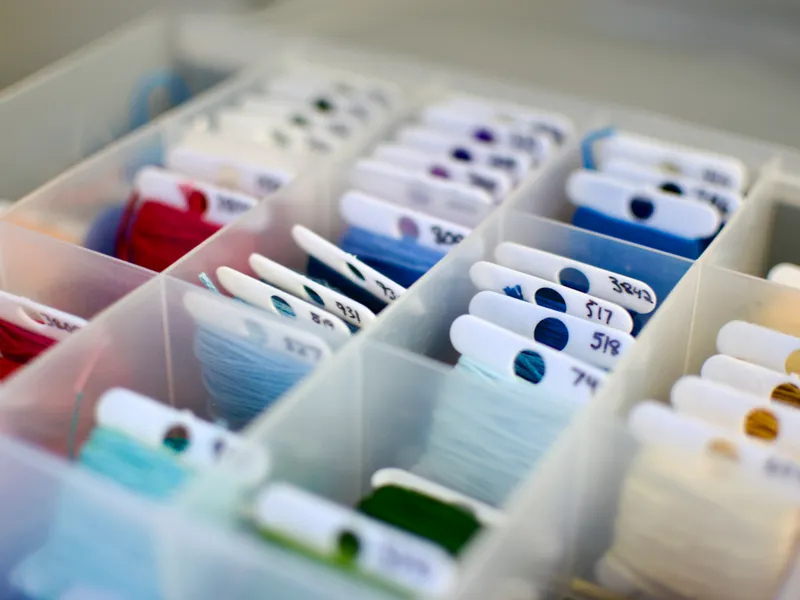
I’m getting back into cross-stitch, so I’ve updated my inventory of DMC embroidery floss colours.

The CRC Handbook of Chemistry and Physics is a 2600-page tome of random facts and figures, from the speed of sound in various media to the chemical composition of the human body.
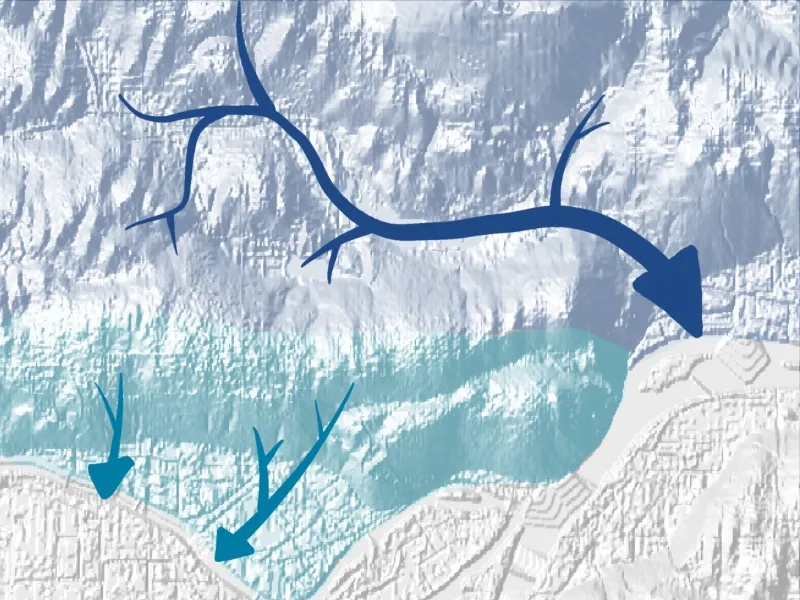
I’m on a quest to explore the creeks and waterways of Vancouver, Burnaby, and New Westminster.

This picture illustrates the danger of poorly-designed streets, which the Swedish government set out to improve in the 1990s.

If you see a coyote in Vancouver, the officially recommended course of action is to yell “Go away coyote.”

Welcome to the newest version of RossChurchley.com! I’ve had this website since 2005 and this is the sixteenth time I’ve rewritten it with a new tech stack.

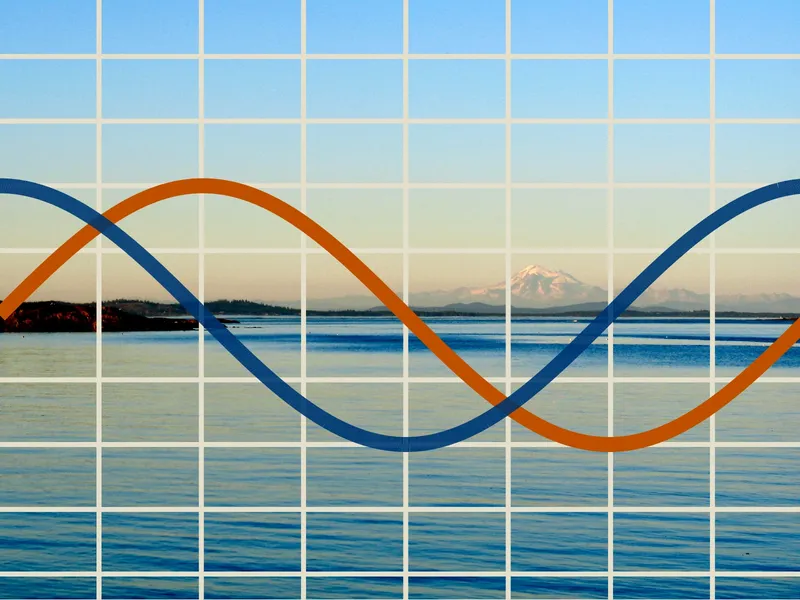
You can get a really good approximation of a sinusoidal curve from twelve equally-spaced line segments of slope 1/12, 2/12, 3/12, 3/12, 2/12, 1/12, -1/12, -2/12, -3/12, -3/12, -2/12, and -1/12, respectively.

Do you got plans tonight?
Song’s “a couple of hundred miles from Japan”, but I —
I was thinking other lyrics mean that can’t be right,
And I can’t get this off of my mind.
The time it takes to properly roast a whole turkey is proportional to its weight to the ⅔ power.


“General particulars” is an excellent phrase that deserves to catch on more widely than its current context of legally-mandated notices on boats.

The head of a sunflower is actually hundreds of smaller flowers working together to attract pollinators. Each large yellow petal is its own individual flower, and the bits in the middle are tiny five-pointed flowers if you look closely.




Not all 26 letters of the alphabet appear on BC license plates. Six are missing — and the reason goes all the way back to 1970, when BC switched from issuing sequential plate numbers to an alphanumeric system.






At first they deployed a man with a stick. The groundsman approached one buzzing batch, decided his mode of attack would not work, and returned defeated.

In collaboration with the SFU Library and my fellow grad students, I’ve written a LaTeX template from which graduate students at Simon Fraser University can start writing their thesis or dissertation.

We were originally just going to model real cities, but we quickly realized there were way too many parking lots in the real world and that [SimCity] was going to be really boring if it was proportional in terms of parking lots.

I defend my thesis in two weeks, but I’ll be prepared for the snake fight portion thanks to McSweeney’s guide.
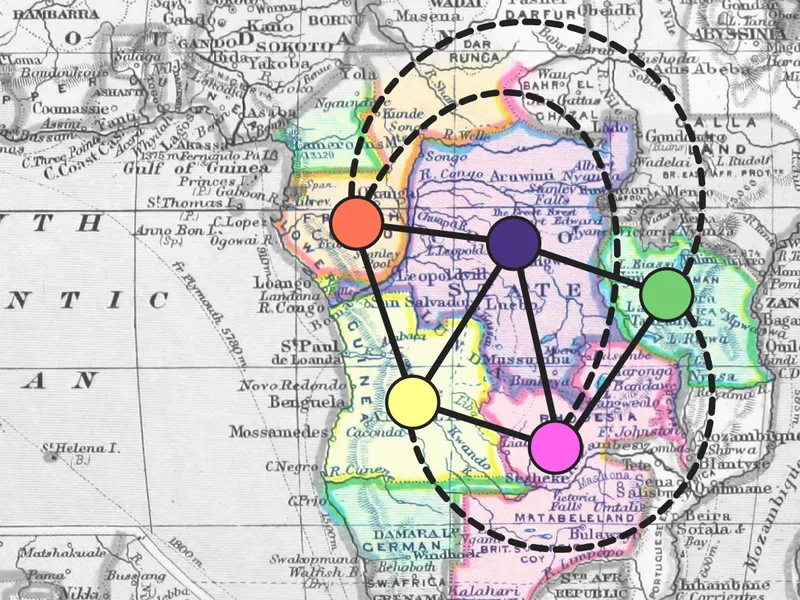
In 1852, then-student Francis Guthrie wondered any if possible map required more than four colours. By the end of the century, Guthrie and his fellow colonists had drawn a map on Africa that needed five.

My Lords, I do not actually deal with the economy. I am glad to say that that would be above my pay grade, whereas trying to deal with the mice is probably just about right for me.