Ore’s Theorem

A red-blue K_n:
bluest Hamilton circuit
lies fully in G.

Ore’s theorem states:

Let G be a simple graph on n ≥ 3 vertices such that d(u) + d(v) ≥ n for any nonadjacent u, v. Then G contains a Hamilton cycle.

Bondy’s proof is roughly as follows. Colour the edges of G blue and add red edges to make a complete graph. The complete graph on n ≥ 3 vertices has no shortage of Hamilton cycles, so choose one and label it v₁v₂…v_nv₁.

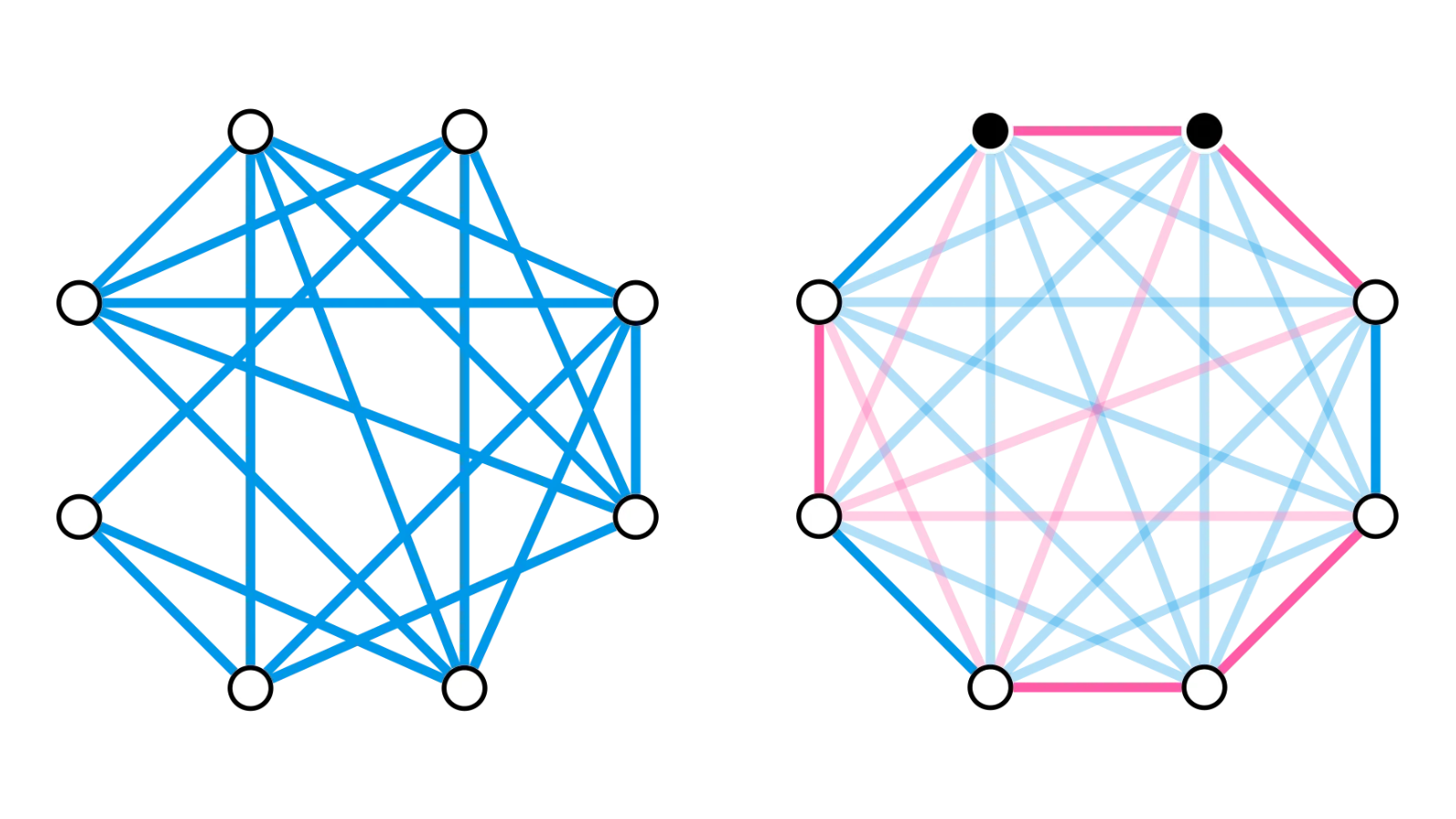
Consider the blue neighbours of v₁ on the cycle, and then move one vertex to the right along the cycle so you’re looking at the set

S = \{ v_{i+1}: v_1 v_i \in E(G) \}

There are d_G(v₁) of these vertices, and if v₁v₂ is red (i.e. v₁ and v₂ are nonadjacent in G), then the theorem’s hypothesis tells us that

|S| = d_G(v_1) \geq n - d_G(v_2).

Since v₂ has only n−1−d_G(v₂) red neighbours and is not itself in S, that means at least one vertex v_i+1 in S is a blue neighbour of v₂. We can now replace v₁v₂ and v_iv_i+1 in the cycle with the two blue edges v₁v₂ and v₂v_i+1 to get a Hamilton cycle of K_n with at least one more blue edge than we had before.

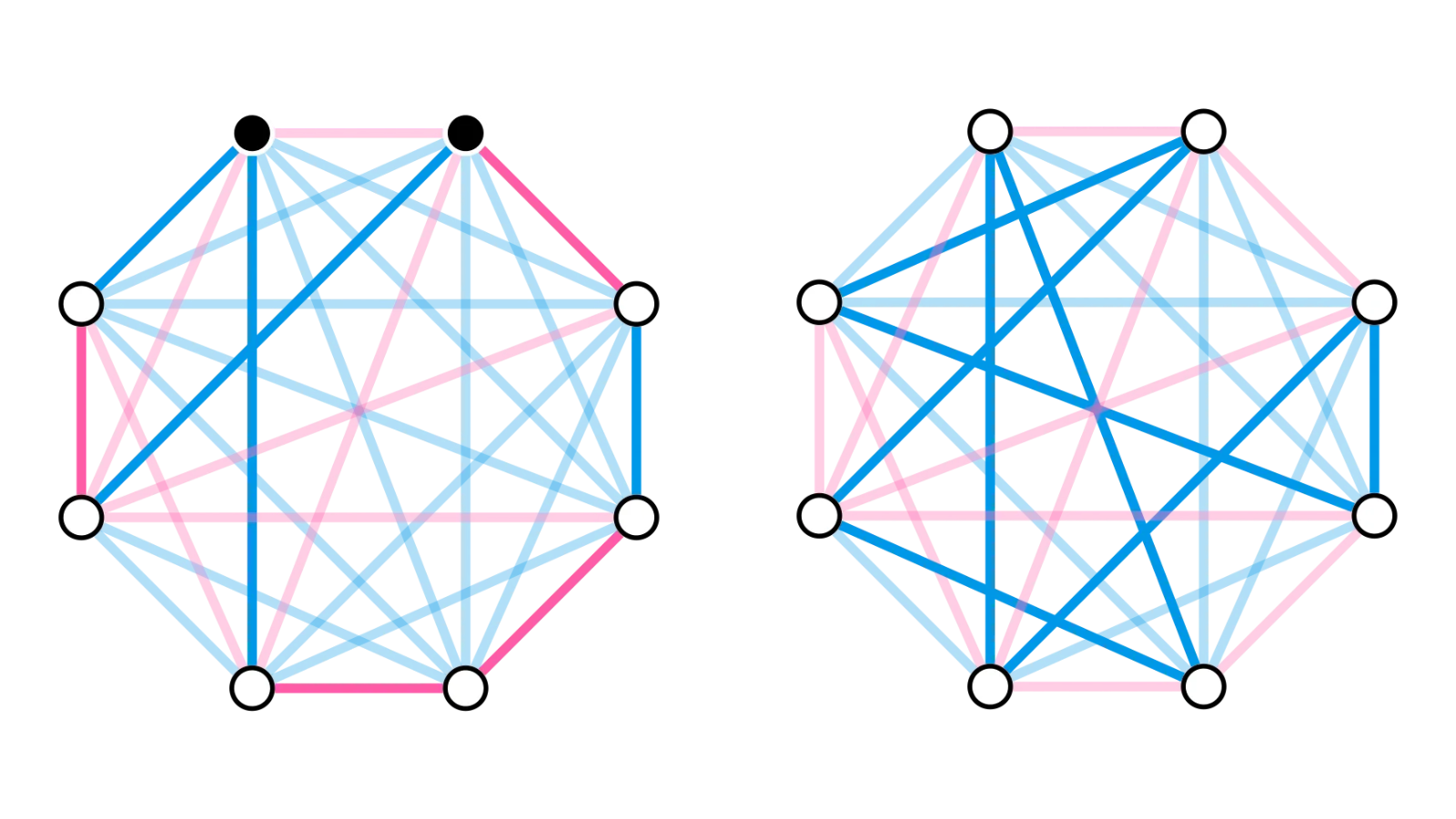
We can make the same argument again and again until we have a Hamilton cycle of K_n with no red edges. The cycle being blue means it lies entirely in G, which proves the theorem.

Pages: 1 2 3 4